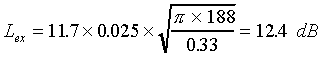|

|
|
|
|
|
|
|
|
|

|
|
ICTP
- URSI
SCHOOL ON DIGITAL AND MULTIMEDIA COMMUNICATIONS USING
TERRESTRIAL AND SATELLITE RADIO
LINKS
12th
February - 2nd March
2001 ,
Trieste
(Italy)
|
|
|
-
|
|
|
|
|
|
|
|
|
A Primer for Digital Experimenters
|
|
|
|
|
Barry McLarnon, VE3JF,
ve3jf@tapr.org
2696 Regina St. Ottawa, ON K2B
6Y1
Abstract
This paper attempts to provide
some insight into the nature of radio propagation in that part of the
spectrum (upper VHF to microwave) used by experimenters for
high-speed digital transmission. It begins with the basics of free
space path loss calculations, and then considers the effects of
refraction, diffraction and reflections on the path loss of Line of
Sight (LOS) links. The nature of non-LOS radio links is then
examined, and propagation effects other than path loss which are
important in digital transmission are also described.
Introduction
The nature of packet radio is
changing. As access to the Internet becomes cheaper and faster, and
the applications offered on the "net" more and more enticing,
interest in the amateur packet radio network which grew up in the
1980s steadily wanes. To be sure, there are still pockets of interest
in some places, particularly where some infrastructure to support
speeds of 9600 bps or more has been built up, but this has not
reversed the trend of declining interest and participation.
Nevertheless, there is still lots of interest in packet radio
out there - it is simply becoming re-focused in different areas. Some
applications which do not require high speed, and can take advantage
of the mobility that packet radio can provide, have found a secure
niche - APRS is a good example. Interest is also high in high-speed
wireless transmission which can match, or preferably exceed, landline
modem rates. With a wireless link, you can have a 24-hour network
connection without the need for a dedicated line, and you may also
have the possibility of portable or mobile operation. Until recently,
most people have considered it to be just too difficult to do
high-speed digital. For example, the WA4DSY 56 Kbps RF modem has been
available for ten years now, and yet only a few hundred people at
most have put one on the air. With the new version of the modem
introduced last year, 56 Kbps packet radio has edged closer to plug
'n play, but in the meantime, landline modem data rates have moved
into the same territory. What has really sparked interest in
high-speed packet radio lately is not the amateur packet equipment,
but the boom in spread spectrum (SS) wireless LAN (WLAN) hardware
which can be used without a licence in some of the ISM bands. The new
WLAN units are typically integrated radio/modem/computer interfaces
which mimic either ethernet interfaces or landline modems, and are
just as easy to set up. Many of them offer speeds which landline
modem users can only dream of. TAPR and others are working on
bringing this type of SS technology into the amateur service, where
it can be used on different bands, and without the Effective Radiated
Power (ERP) restrictions which exist for the unlicenced service. This
technology will be the ticket to developing high-speed wireless LANs
and MANs which, using the Internet as a backbone, could finally
realize the dream of a high-performance wide-area AMPRnet which can
support the applications (WWW, audio and video conferencing, etc.)
that get people excited about computer networking these days.
Although the dream as stated above
is somewhat controversial, the author believes it represents the best
hope of attracting new people to the hobby, providing a basis for
experimentation and training in state-of-the-art wireless techniques
and networking, and, ultimately, retaining spectrum for the amateur
radio service. One problem is that most of the people attracted to
using digital wireless techniques have little or no background in RF.
When it comes to setting up wireless links which will work over some
distance, they tend to lack the necessary knowledge about antennas,
transmission lines and, especially, the subtleties of radio
propagation. This paper deals with the latter area, in the hopes of
providing this new crop of digital experimenters with some tools to
help them build wireless links which work.
The main emphasis of this paper is
on predicting the path loss of a link, so that one can approach the
installation of the antennas and other RF equipment with some degree
of confidence that the link will work. The focus is on acquiring a
feel for radio propagation, and pointing the way towards recognizing
the alternatives that may exist and the instances in which
experimentation may be fruitful. We'll also look at some propagation
aspects which are of particular relevance to digital
signaling.
Estimating Path
Loss
The fundamental aim of a radio
link is to deliver sufficient signal power to the receiver at the far
end of the link to achieve some performance objective. For a data
transmission system, this objective is usually specified as a minimum
bit error rate (BER). In the receiver demodulator, the BER is a
function of the signal to noise ratio (SNR). At the frequencies under
consideration here, the noise power is often dominated by the
internal receiver noise; however, this is not always the case,
especially at the lower (VHF) end of the range. In addition, the
"noise" may also include significant power from interfering signals,
necessitating the delivery of higher signal power to the receiver
than would be the case under more ideal circumstances (i.e.,
back-to-back through an attenuator). If the channel contains
multipath, this may also have a major impact on the BER. We will
consider multipath in more detail later - for now, we will focus on
predicting the signal power which will be available to the
receiver.
Free Space
Propagation
The benchmark by which we measure
the loss in a transmission link is the loss that would be expected in
free space - in other words, the loss that would occur in a region
which is free of all objects that might absorb or reflect radio
energy. This represents the ideal case which we hope to approach in
our real world radio link (in fact, it is possible to have path loss
which is less than the "free space" case, as we shall see later, but
it is far more common to fall short of this goal).
Calculating free space
transmission loss is quite simple. Consider a transmitter with power
Pt coupled to an antenna which radiates equally in all
directions (everyone's favorite mythical antenna, the
isotropic antenna). At a distance d from the transmitter, the
radiated power is distributed uniformly over an area of 4 d2
(i.e. the surface area of a sphere of radius d), so that the power
flux density is:
d2
(i.e. the surface area of a sphere of radius d), so that the power
flux density is:
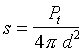 (1)
(1)
The transmission loss then depends
on how much of this power is captured by the receiving antenna. If
the capture area, or effective aperture of this antenna is
Ar, then the power which can be delivered to the
receiver (assuming no mismatch or feedline losses) is simply
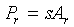 (2)
(2)
For the hypothetical isotropic
receiving antenna, we have
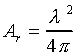 (3)
(3)
Combining equations (1) and (3)
into (2), we have
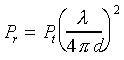 (4)
(4)
The free space path loss between
isotropic antennas is Pt / Pr.
Since we usually are dealing with frequency rather than wavelength,
we can make the substitution = c/f (where c, of course, is the speed
of light) to get
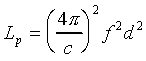 (5)
(5)
This shows the classic square-law
dependence of signal level versus distance. What troubles some people
when they see this equation is that the path loss also increases as
the square of the frequency. Does this mean that the transmission
medium is inherently more lossy at higher frequencies? While it is
true that absorption of RF by various materials (buildings, trees,
water vapor, etc.) tends to increase with frequency, remember we are
talking about "free space" here. The frequency dependence in this
case is solely due to the decreasing effective aperture of the
receiving antenna as the frequency increases. This is intuitively
reasonable, since the physical size of a given antenna type is
inversely proportional to frequency. If we double the frequency, the
linear dimensions of the antenna decrease by a factor of one-half,
and the capture area by a factor of one-quarter. The antenna
therefore captures only one-quarter of the power flux density at the
higher frequency versus the lower one, and delivers 6 dB less signal
to the receiver. However, in most cases we can easily get this 6 dB
back by increasing the effective aperture, and hence the gain, of the
receiving antenna. For example, suppose we are using a parabolic dish
antenna at the lower frequency. When we double the frequency, instead
of allowing the dish to be scaled down in size so as to produce the
same gain as before, we can maintain the same reflector size. This
gives us the same effective aperture as before (assuming that the
feed is properly redesigned for the new frequency, etc.), and 6 dB
more gain (remembering that the gain is with respect to an isotropic
or dipole reference antenna at the same frequency). Thus the
free space path loss is now the same at both frequencies; moreover,
if we maintained the same physical aperture at both ends of
the link, we would actually have 6 dB less path loss at the
higher frequency. You can picture this in terms of being able to
focus the energy more tightly at the frequency with the shorter
wavelength. It has the added benefit of providing greater
discrimination against multipath - more about this later.
The free space path loss equation
is more usefully expressed logarithmically:
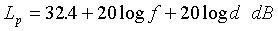 (f in MHz, d in km) (6a)
(f in MHz, d in km) (6a)
or
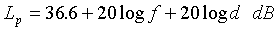 (f in MHz, d in miles) (6b)
(f in MHz, d in miles) (6b)
This shows more clearly the
relationship between path loss and distance: path loss increases by
20 dB/decade or 6 dB/octave, so each time you double the distance,
you lose another 6 dB of signal under free space conditions.
Of course, in looking at a real
system, we must consider the actual antenna gains and cable losses in
calculating the signal power Pr which is available at the
receiver input:
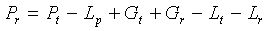 (7)
(7)
where
Pt
= transmitter power output (dBm or dBW, same units as
Pr)
Lp
= free space path loss between isotropic antennas
(dB)
Gt
= transmit antenna gain (dBi)
Gr
= receive antenna gain (dBi)
Lt
= transmission line loss between transmitter and transmit antenna
(dB)
Lr
= transmission line loss between receive antenna and receiver
input (dB)
A table of transmission line
losses for various bands and popular cable types can be found in the
Appendix.
Example 1. Suppose you have
a pair of 915 MHz WaveLAN cards, and want to use them on a 10 km link
on which you believe free space path loss conditions will apply. The
transmitter power is 0.25 W, or +24 dBm. You also have a pair of yagi
antennas with 10 dBi gain, and at each end of the link, you need
about 50 ft (15 m) of transmission line to the antenna. Let's say
you're using LMR-400 coaxial cable, which will give you about 2 dB
loss at 915 MHz for each run. Finally, the path loss from equation
(6a) is calculated, and this gives 111.6 dB, which we'll round off to
112 dB. The expected signal power at the receiver is then, from
(7):
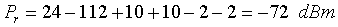
According to the WaveLAN
specifications, the receivers require -78 dBm signal level in order
to deliver a low bit error rate (BER). So, we should be in good
shape, as we have 6 dB of margin over the minimum requirement.
However, this will only be true if the path really is
equivalent to the free space case, and this is a big if! We'll
look at means of predicting whether the free space assumption holds
in the next section.
Path Loss on Line of Sight
Links
The term Line of Sight (LOS) as
applied to radio links has a pretty obvious meaning: the antennas at
the ends of the link can "see" each other, at least in a radio sense.
In many cases, radio LOS equates to optical LOS: you're at the
location of the antenna at one end of the link, and with the unaided
eye or binoculars, you can see the antenna (or its future site) at
the other end of the link. In other cases, we may still have an LOS
path even though we can't see the other end visually. This is because
the radio horizon extends beyond the optical horizon. Radio waves
follow slightly curved paths in the atmosphere, but if there is a
direct path between the antennas which doesn't pass through any
obstacles, then we still have radio LOS. Does having LOS mean that
the path loss will be equal to the free space case which we have just
considered? In some cases, the answer is yes, but it is definitely
not a sure thing. There are three mechanisms which may cause the path
loss to differ from the free space case:
- refraction in the
earth's atmosphere, which alters the trajectory of radio waves,
and which can change with time.
- diffraction effects
resulting from objects near the direct path.
- reflections from
objects, which may be either near or far from the direct
path.
We examine these mechanisms in the
next three sections.
Atmospheric
Refraction
As mentioned previously, radio
waves near the earth's surface do not usually propagate in precisely
straight lines, but follow slightly curved paths. The reason is
well-known to VHF/UHF DXers: refraction in the earth's atmosphere.
Under normal circumstances, the index of refraction decreases
monotonically with increasing height, which causes the radio waves
emanating from the transmitter to bend slightly downwards towards the
earth's surface instead of following a straight line. The effect is
more pronounced at radio frequencies than at the wavelength of
visible light, and the result is that the radio waves can propagate
beyond the optical horizon, with no additional loss other than the
free space distance loss. There is a convenient artifice which is
used to account for this phenomenon: when the path profile is
plotted, we reduce the curvature of the earth's surface. If we choose
the curvature properly, the paths of the radio waves can be plotted
as straight lines. Under normal conditions, the gradient in
refractivity index is such that real world propagation is equivalent
to straight-line propagation over an earth whose radius is greater
than the real one by a factor of 4/3 - thus the often-heard term "4/3
earth radius" in discussions of terrestrial propagation. However,
this is just an approximation that applies under typical conditions -
as VHF/UHF experimenters well know, unusual weather conditions can
change the refractivity profile dramatically. This can lead to
several different conditions. In superrefraction, the rays
bend more than normal and the radio horizon is extended; in extreme
cases, it leads to the phenomenon known as ducting, where the
signal can propagate over enormous distances beyond the normal
horizon. This is exciting for DXers, but of little practical use for
people who want to run data links. The main consequence for digital
experimenters is that they may occasionally experience interference
from unexpected sources. A more serious concern is
subrefraction, in which the bending of the rays is less than
normal, thus shortening the radio horizon and reducing the clearance
over obstacles along the path. This may lead to increased path loss,
and possibly even an outage. In commercial radio link planning, the
statistical probability of these events is calculated and allowed for
in the link design (distance, path clearance, fading margin, etc.).
We won't get into all of the details here; suffice it to say that
reliability of your link will tend to be higher if you back off the
distance from the maximum which is dictated by the normal radio
horizon. Not that you shouldn't try and stretch the limits when the
need arises, but a link which has optical clearance is preferable to
one which doesn't. It's also a good idea to build in some margin to
allow for fading due to unusual propagation situations, and to allow
as much clearance from obstacles along the path as possible. For
short-range links, the effects of refraction can usually be
ignored.
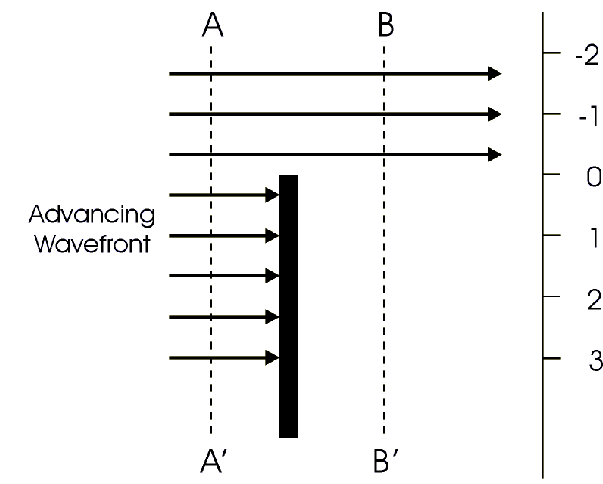
Figure 1 Shadowing of
Radio Waves by an Object
Diffraction and Fresnel
Zones
Refraction and reflection of radio
waves are mechanisms which are fairly easy to picture, but
diffraction is much less intuitive. To understand diffraction, and
radio propagation in general, it is very helpful to have some feeling
for how radio waves behave in an environment which is not strictly
"free space". Consider Fig. 1, in which a wavefront is traveling from
left to right, and encountering an obstacle which absorbs or reflects
all of the incident radio energy. Assume that the incident wavefront
is uniform; i.e., if we measure the field strength along the line
A-A', it is the same at all points. Now, what will be the field
strength along a line B-B' on the other side of the obstacle? To
quantify this, we provide an axis in which zero coincides with the
top of the obstacle, and negative and positive numbers denote
positions above and below this, respectively (we'll define the
parameter used on this axis a bit later).
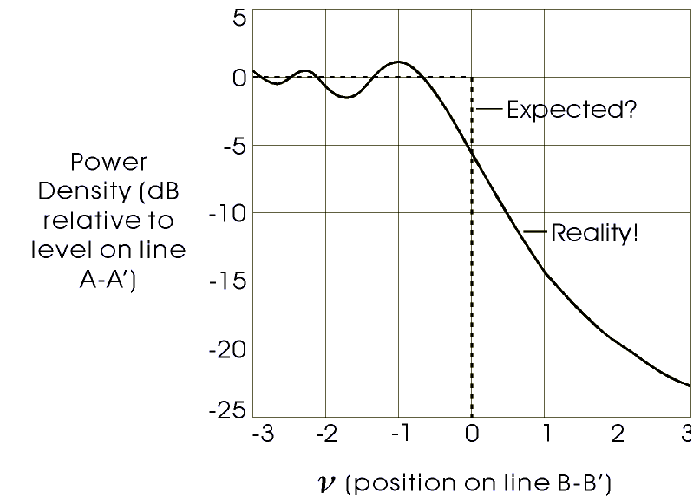
Figure 2 Signal Levels
on the Far Side of the Shadowing Object
Intuition may lead one to expect
the field strength along B-B' to look like the dashed line in Fig. 2,
with complete shadowing and zero signal below the top of the
obstacle, and no effect at all above it. The solid line shows the
reality: not only does energy "leak" into the shadowed area, but the
field strength above the top of the obstacle is also disturbed. At a
position which is level with the top of the obstacle, the signal
power density is down by some 6 dB, despite the fact that this point
is in "line of sight" of the source. This effect is less surprising
when one considers other familiar instances of wave motion. Picture,
for example, tossing a rock in a pond and watching the ripples
propagate outward. When they encounter an object such as a boat or a
pier, you will see that the water behind the object is also
disturbed, and that the waves traveling past, but close to, the
object are also affected somewhat. Similarly, consider a distant
source of sound waves: if the sound level is well above the ambient
level, then moving behind an object which absorbs the incident sound
energy completely does not result in the sound disappearing
completely - it is still audible at a lower level, due to diffraction
(as an aside, it is interesting to note that the wavelength of a 1
KHz sound wave is nearly the same as a 1 GHz radio wave). So much for
analogies - let's get back to radio waves.
The explanation for the
non-intuitive behavior of radio waves in the presence of obstacles
which appear in their path is found in something called Huygens'
Principle. Huygens showed that propagation occurs as follows:
each point on a wavefront acts as a source of a secondary wavefront
known as a wavelet, and a new wavefront is then built up from
the combination of the contributions from all of the wavelets on the
preceding wavefront. The secondary wavelets do not radiate equally in
all directions - their amplitude in a given direction is proportional
to (1 + cos a), where a is the angle between that
direction and the direction of propagation of the wavefront. The
amplitude is therefore maximum in the direction of propagation (i.e.,
normal to the wavefront), and zero in the reverse direction. The
representation of a wavefront as a collection of wavelets is shown in
Fig. 3.
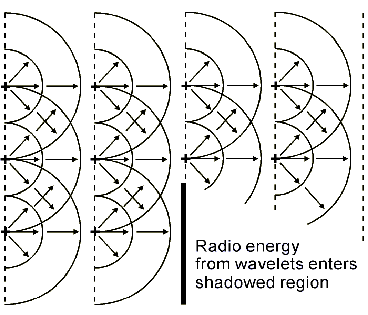
Figure 3
Representation of Radio Waves as
Wavelets
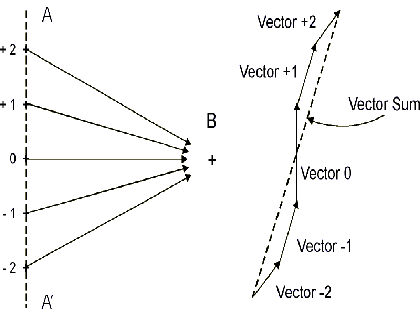
Figure 4 Building of a New
Wavefront by Vector Summation
At a given point on the new
wavefront (point B), the signal vector (phasor) is determined by
vector addition of the contributions from the wavelets on the
preceding wavefront, as shown in Fig. 4. The largest component is
from the nearest wavelet, and we then get symmetrical contributions
from the points above and below it. These latter vectors are shorter,
due to the angular reduction of amplitude mentioned above, and also
the greater distance traveled. The greater distance also introduces
more time delay, and hence the rotation of the vectors as shown in
the figure. As we include contributions from points farther and
farther away, the corresponding vectors continue to rotate and
diminish in length, and they trace out a double-sided spiral path,
known as the Cornu spiral.
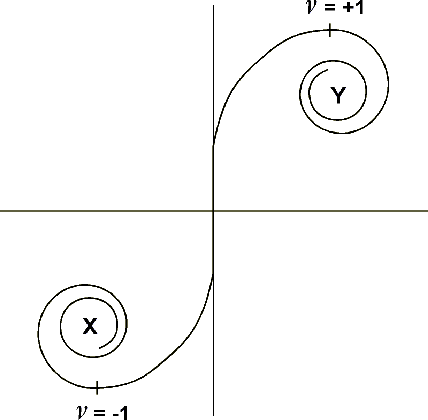
Figure 5 The Cornu
Spiral
The Cornu spiral, shown in Fig. 5,
provides the tool we need to visualize what happens when radio waves
encounter an obstacle. In free space, at every point on a new
wavefront, all contributions from the wavelets on the preceding
wavefront are present and unattenuated, so the resultant vector
corresponds to the complete spiral (i.e., the endpoints of the vector
are X and Y). Now, consider again the situation shown in Fig. 1, and
for each location on the wavefront B-B', visualize the makeup of the
Cornu spiral (note that the top of the obstacle is assumed to be
sufficiently narrow that no significant reflections can occur from
it). At position 0, level with the top of the obstacle, we will have
only contributions from the positive half of the preceding wavefront
at A-A', since all of the others are blocked by the obstacle.
Therefore, the received components form only the upper half of the
spiral, and the resultant vector is exactly half the length of the
free space case, corresponding to a 6 dB reduction in amplitude. As
we go lower on the line B-B', we start to get blockage of components
from the positive side of the A-A' wavefront, removing more and more
of the vectors as we go, and leaving only the tight upper spiral. The
resulting amplitude diminishes monotonically towards zero as we move
down the new wavefront, but there is still signal present at
all points behind the obstacle, as shown in the graph in Fig. 2. How
about the points along line B-B' above the obstacle, where the
graph shows those mysterious ripples? Again, look at the Cornu
spiral: as we move up the line, we begin to add contributions from
the negative side of the A-A' wavefront (vectors -1, -2, etc.). Note
what happens to the resultant vector - as we make the first turn
around the bottom of the spiral, it reaches its maximum length,
corresponding to the highest peak in the graph of Fig. 2. As we
continue to move up B-B' and add more components, we swing around the
spiral and reach the minimum length for the resultant vector (minimum
distance from point Y). Further progression up B-B' results in
further motion around the spiral, and the amplitude of the resultant
oscillates back and forth, with the amplitude of the oscillation
steadily decreasing as the resultant converges on the free space
value, given by the complete Cornu spiral (vector X-Y).
So, in a nutshell, to visualize
what happens to radio waves when they encounter an obstacle, we have
to develop a picture of the wavefront after the obstacle as a
function of the wavefront just before it (as opposed to simply
tracing rays from the distant source). Now we're in a position to
talk about Fresnel zones. A Fresnel zone is a simpler concept once
you have some understanding of diffraction: it is the volume of space
enclosed by an ellipsoid which has the two antennas at the ends of a
radio link at its foci. The two-dimensional representation of a
Fresnel zone is shown in Fig. 6. The surface of the ellipsoid is
defined by the path ACB, which exceeds the length of the direct path
AB by some fixed amount. This amount is n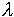 /2,
where n is a positive integer. For the first Fresnel zone, n = 1 and
the path length differs by
/2,
where n is a positive integer. For the first Fresnel zone, n = 1 and
the path length differs by 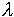 /2
(i.e., a 180 phase reversal with respect to the direct path). For
most practical purposes, only the first Fresnel zone need be
considered. A radio path has first Fresnel zone clearance if,
as shown in Fig. 6, no objects capable of causing significant
diffraction penetrate the corresponding ellipsoid. What does this
mean in terms of path loss? Recall how we constructed the wavefront
behind an object by vector addition of the wavelets comprising the
wavefront in front of the object, and apply this to the case where we
have exactly first Fresnel zone clearance. We wish to find the
strength of the direct path signal after it passes the object.
Assuming there is only one such object near the Fresnel zone, we can
look at the resultant wavefront at the destination point B. In terms
of the Cornu spiral, the upper half of the spiral is intact, but part
of the lower half is absent, due to blockage by the object. Since we
have exactly first Fresnel clearance, the final vector which we add
to the bottom of the spiral is 180 degrees out of phase with the
direct-path vector - i.e., it is pointing downwards. This means that
we have passed the bottom of the spiral and are on the way back up,
and the resultant vector is near the free space magnitude (a line
between X and Y in Fig. 5). In fact, it is sufficient to have 60% of
the first Fresnel clearance, since this will still give a resultant
which is very close to the free space value.
/2
(i.e., a 180 phase reversal with respect to the direct path). For
most practical purposes, only the first Fresnel zone need be
considered. A radio path has first Fresnel zone clearance if,
as shown in Fig. 6, no objects capable of causing significant
diffraction penetrate the corresponding ellipsoid. What does this
mean in terms of path loss? Recall how we constructed the wavefront
behind an object by vector addition of the wavelets comprising the
wavefront in front of the object, and apply this to the case where we
have exactly first Fresnel zone clearance. We wish to find the
strength of the direct path signal after it passes the object.
Assuming there is only one such object near the Fresnel zone, we can
look at the resultant wavefront at the destination point B. In terms
of the Cornu spiral, the upper half of the spiral is intact, but part
of the lower half is absent, due to blockage by the object. Since we
have exactly first Fresnel clearance, the final vector which we add
to the bottom of the spiral is 180 degrees out of phase with the
direct-path vector - i.e., it is pointing downwards. This means that
we have passed the bottom of the spiral and are on the way back up,
and the resultant vector is near the free space magnitude (a line
between X and Y in Fig. 5). In fact, it is sufficient to have 60% of
the first Fresnel clearance, since this will still give a resultant
which is very close to the free space value.

Figure 6 Fresnel Zone
for a Radio Link
In order to quantify diffraction
losses, they are usually expressed in terms of a dimensionless
parameter , given by:
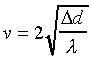 (8)
(8)
where 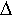 d
is the difference in lengths of the straight-line path between the
endpoints of the link and the path which just touches the tip of the
diffracting object (see Fig. 7, where
d
is the difference in lengths of the straight-line path between the
endpoints of the link and the path which just touches the tip of the
diffracting object (see Fig. 7, where 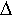 d
= d1 + d2 - d). By convention,
d
= d1 + d2 - d). By convention, 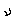 is positive when the direct path is blocked (i.e., the obstacle has
positive height), and negative when the direct path has some
clearance ("negative height"). When the direct path just grazes the
object,
is positive when the direct path is blocked (i.e., the obstacle has
positive height), and negative when the direct path has some
clearance ("negative height"). When the direct path just grazes the
object, 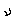 = 0. This
is the parameter shown in Figures 1 and 2. Since in this section we
are considering LOS paths, this corresponds to specifying that
= 0. This
is the parameter shown in Figures 1 and 2. Since in this section we
are considering LOS paths, this corresponds to specifying that
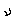 is negative (or
zero). For first Fresnel zone clearance, we have
is negative (or
zero). For first Fresnel zone clearance, we have 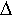 d
=
d
= 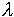 /2, so from
equation (8),
/2, so from
equation (8), 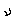 =
-1.4. From Fig. 2, we can see that this is more clearance than
necessary - in fact, we get slightly higher signal level (and path
loss less than the free space value) if we reduce the clearance to
=
-1.4. From Fig. 2, we can see that this is more clearance than
necessary - in fact, we get slightly higher signal level (and path
loss less than the free space value) if we reduce the clearance to
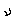 = -1, which
corresponds to
= -1, which
corresponds to 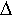 d
=
d
= 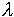 /4. The
/4. The
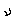 = -1 point is also
shown on the Cornu spiral in Fig. 5. Since
= -1 point is also
shown on the Cornu spiral in Fig. 5. Since 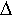 d=
d=
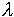 /4, the last
vector added to the summation is rotated 90 from the direct-path
vector, which brings us to the lowest point on the spiral. The
resultant vector then runs from this point to the upper end of the
spiral at point Y. It's easy to see that this vector is a bit longer
than the distance from X to Y, so we have a slight gain (about 1.2
dB) over the free space case. We can also see how we can back off to
60% of first Fresnel zone clearance (
/4, the last
vector added to the summation is rotated 90 from the direct-path
vector, which brings us to the lowest point on the spiral. The
resultant vector then runs from this point to the upper end of the
spiral at point Y. It's easy to see that this vector is a bit longer
than the distance from X to Y, so we have a slight gain (about 1.2
dB) over the free space case. We can also see how we can back off to
60% of first Fresnel zone clearance (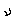 = -0.85) without suffering significant loss.
= -0.85) without suffering significant loss.
But how do we calculate whether we
have the required clearance? The geometry for Fresnel zone
calculations is shown in Fig. 7. Keep in mind that this is only a
two-dimensional representation, but Fresnel zones are
three-dimensional. The same considerations apply when the objects
limiting path clearance are to the side or even above the radio path.
Since we are considering LOS paths in this section, we are dealing
only with the "negative height" case, shown in the lower part of the
figure. We will look at the case where h is positive later, when we
consider non-LOS paths.
For first Fresnel zone clearance,
the distance h from the nearest point of the obstacle to the direct
path must be at least
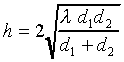 (9)
(9)
where d1 and
d2 are the distances from the tip of the obstacle to the
two ends of the radio circuit. This formula is an approximation which
is not valid very close to the endpoints of the circuit. For
convenience, the clearance can be expressed in terms of
frequency:
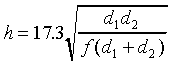 (10a)
(10a)
where f is the frequency in GHz,
d1 and d2 are in km, and h is in meters.
Or:
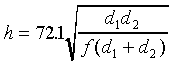 (10b)
(10b)
where f is in GHz, d1
and d2 in statute miles, and h is in feet.
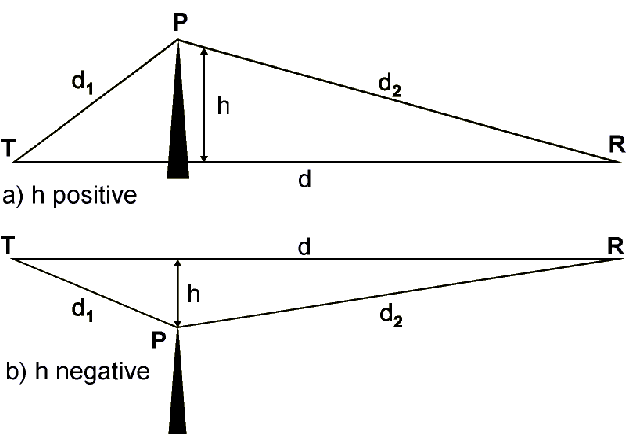
Figure 7 Fresnel Zone
Geometry
Example 2. We have a 10 km
LOS path over which we wish to establish a link in the 915 MHz band.
The path profile indicates that the high point on the path is 3 km
from one end, and the direct path clears it by about 18 meters (60
ft.) - do we have adequate Fresnel zone clearance? From equation
(10a), with d1 = 3 km, d2 = 7 km, and f = 0.915
GHz, we have h = 26.2 m for first Fresnel zone clearance (strictly
speaking, h = -26.2 m). A clearance of 18 m is about 70% of this, so
it is sufficient to allow negligible diffraction loss.
Fresnel zone clearance may not
seem all that important - after all, we said previously that for the
zero clearance (grazing) case, we have 6 dB of additional path loss.
If necessary, this could be overcome with, for example, an additional
3 dB of antenna gain at each end of the circuit. Now it's time to
confess that the situation depicted in Figures 1 and 2 is a special
case, known as "knife edge" diffraction. Basically, this means that
the top of the obstacle is small in terms of wavelengths. This is
sometimes a reasonable approximation of an object in the real
world, but more often than not, the obstacle will be rounded (such as
a hilltop) or have a large flat surface (like the top of a building),
or otherwise depart from the knife edge assumption. In such cases,
the path loss for the grazing case can be considerably more than 6 dB
- in fact, 20 dB would be a better estimate in many cases. So,
Fresnel zone clearance can be pretty important on real-world paths.
And, again, keep in mind that the Fresnel zone is three-dimensional,
so clearance must also be maintained from the sides of buildings,
etc. if path loss is to be minimized. Another point to consider is
the effect on Fresnel zone clearance of changes in atmospheric
refraction, as discussed in the last section. We may have adequate
clearance on a longer path under normal conditions (i.e., 4/3 earth
radius), but lose the clearance when unusual refraction conditions
prevail. On longer paths, therefore, it is common in commercial radio
links to do the Fresnel zone analysis on something close to "worst
case" rather than typical refraction conditions, but this may be less
of a concern in amateur applications.
Most of the material in this
section was based on Ref. [2], which is highly recommended
for further reading.
Ground Reflections
An LOS path may have adequate
Fresnel zone clearance, and yet still have a path loss which differs
significantly from free space under normal refraction conditions. If
this is the case, the cause is probably multipath propagation
resulting from reflections (multipath also poses particular problems
for digital transmission systems - we'll look at this a bit later,
but here we are only considering path
loss).
One common source of reflections
is the ground. It tends to be more of a factor on paths in rural
areas; in urban settings, the ground reflection path will often be
blocked by the clutter of buildings, trees, etc. In paths over
relatively smooth ground or bodies of water, however, ground
reflections can be a major determinant of path loss. For any radio
link, it is worthwhile to look at the path profile and see if the
ground reflection has the potential to be significant. It should also
be kept in mind that the reflection point is not at the midpoint of
the path unless the antennas are at the same height and the ground is
not sloped in the reflection region - just the remember the old maxim
from optics that the angle of incidence equals the angle of
reflection.
Ground reflections can be good
news or bad news, but are more often the latter. In a radio path
consisting of a direct path plus a ground-reflected path, the path
loss depends on the relative amplitude and phase relationship of the
signals propagated by the two paths. In extreme cases, where the
ground-reflected path has Fresnel clearance and suffers little loss
from the reflection itself (or attenuation from trees, etc.), then
its amplitude may approach that of the direct path. Then, depending
on the relative phase shift of the two paths, we may have an
enhancement of up to 6 dB over the direct path alone, or cancellation
resulting in additional path loss of 20 dB or more. If you are
acquainted with Mr. Murphy, you know which to expect! The difference
in path lengths can be estimated from the path profile, and then
translated into wavelengths to give the phase relationship. Then we
have to account for the reflection itself, and this is where things
get interesting. The amplitude and phase of the reflected wave depend
on a number of variables, including conductivity and permittivity of
the reflecting surface, frequency, angle of incidence, and
polarization.
It is difficult to summarize the
effects of all of the variables which affect ground reflections, but
a typical case is shown in Fig. 8 [2]. This particular figure
is for typical ground conditions at 100 MHz, but the same behavior is
seen over a wide range of ground constants and frequencies. Notice
that there is a large difference in reflection amplitudes between
horizontal and vertical polarization (denoted on the curves with "h"
and "v", respectively), and that vertical polarization in general
gives rise to a much smaller reflected wave. However, the difference
is large only for angles of incidence greater than a few degrees
(note that, unlike in optics, in radio transmission the angle of
incidence is normally measured with respect to a tangent to the
reflecting surface rather than a normal to it); in practice, these
angles will only occur on very short paths, or paths with
extraordinarily high antennas. For typical paths, the angle of
incidence tends to be of the order of one degree or less - for
example, for a 10 km path over smooth earth with 10 m antenna
heights, the angle of incidence of the ground reflection would only
be about 0.11 degrees. In such a case, both polarizations will give
reflection amplitudes near unity (i.e., no reflection loss). Perhaps
more surprisingly, there will also be a phase reversal in both cases.
Horizontally-polarized waves always undergo a phase reversal upon
reflection, but for vertically-polarized waves, the phase change is a
function of the angle of incidence and the ground
characteristics.
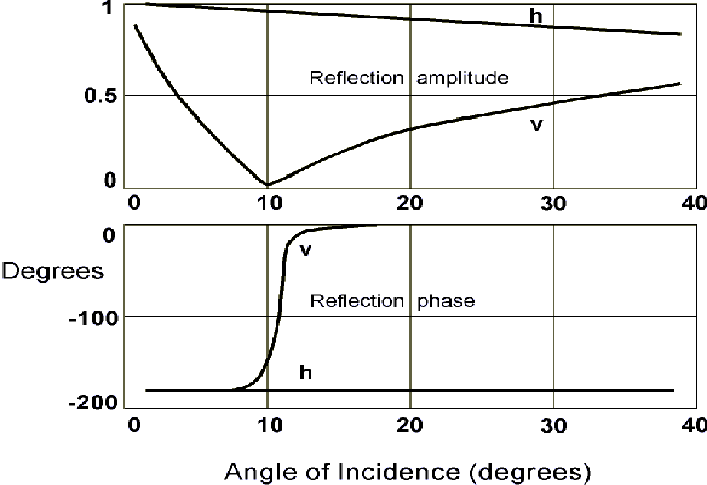
Figure 8 Typical
Ground Reflection Parameters
The upshot of all this is that for
most paths in which the ground reflection is significant (and no
other reflections are present), there will be very little difference
in performance between horizontal and vertical polarization. For very
short paths, horizontal polarization will generally give rise to a
stronger reflection. If it turns out that this causes cancellation
rather than enhancement, switching to vertical polarization may
provide a solution. In other words, for shorter paths, it is usually
worthwhile to try both polarizations to see which works better (of
course, other factors such as mounting constraints and rejection of
other sources of multipath and interference also enter into the
choice of polarization).
As stated above, for either
polarization, as the path gets longer we approach the case where the
ground reflection produces a phase reversal and very little
attenuation. At the same time, the direct and reflected paths are
becoming more nearly equal. The path loss ripples up and down as we
increase the distance, until we reach the point where the path
lengths differ by just one-half wavelength. Combined with the
180° phase shift caused by the ground reflection, this brings
the direct and reflected signals into phase, resulting in an
enhancement over the free space path loss (theoretically 6 dB, but
this will seldom be realized in practice). Thereafter, it's all
downhill as the distance is further increased, since phase difference
between the two paths approaches in the limit the 180° phase
shift of the ground reflection. It can be shown that, in this region,
the received power follows an inverse fourth-power law as a function
of distance instead of the usual square law (i.e., 12 dB more
attenuation when you double the distance, instead of 6 dB). The
distance at which the path loss starts to increase at the
fourth-power rate is reached when the ellipsoid corresponding to the
first Fresnel zone just touches the ground. A reasonably good
estimate of this distance can be calculated from the
equation
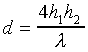 (11)
(11)
where h1 and
h2 are the antenna heights above the ground reflection
point. For example, for antenna heights of 10 m, at 915 MHz
( = 33 cm) we
will be into the fourth-law loss region for links longer than about
1.2 km.
= 33 cm) we
will be into the fourth-law loss region for links longer than about
1.2 km.
So, for longer-range paths, ground
reflections are always bad news. Serious problems with ground
reflections are most commonly encountered with radio links across
bodies of water. Spread spectrum techniques and diversity antenna
arrangements usually can't overcome the problems - the solution lies
in siting the antennas (e.g., away from the shore of the body of
water) such that the reflected path is cut off by natural obstacles,
while the direct path is unimpaired. In other cases, it may be
possible to adjust the antenna locations so as to move the reflection
point to a rough area of land which scatters the signal rather than
creating a strong specular reflection.
Other Sources of
Reflections
Much of what has been said about
ground reflections applies to reflections from other objects as well.
The "ground reflection" on a particular path may be from a building
rooftop rather than the ground itself, but the effect is much the
same. On long links, reflections from objects near the line of the
direct path will almost always cause increased path loss - in
essence, you have a permanent "flat fade" over a very wide bandwidth.
Reflections from objects which are well off to the side of the direct
path are a different story, however. This is a frequent occurrence in
urban areas, where the sides of buildings can cause strong
reflections. In such cases, the angle of incidence may be much larger
than zero, unlike the ground reflection case. This means that
horizontal and vertical polarization may behave quite differently -
as we saw in Fig. 8, vertically polarized signals tend to produce
lower-amplitude reflections than horizontally polarized signals when
the angle of incidence exceeds a few degrees. When the reflecting
surface is vertical, like the side of a building, a signal which is
transmitted with horizontal polarization effectively has vertical
polarization as far as the reflection is concerned. Therefore,
horizontal polarization will generally result in weaker reflections
and less multipath than vertical polarization in these
cases.
Effects of Rain, Snow and
Fog
The loss of LOS paths may
sometimes be affected by weather conditions (other than the
refraction effects which have already been mentioned). Rain and fog
(clouds) become a significant source of attenuation only when we get
well into the microwave region. Attenuation from fog only becomes
noticeable (i.e., attenuation of the order of 1 dB or more) above
about 30 GHz. Snow is in this category as well. Rain attenuation
becomes significant at around 10 GHz, where a heavy rainfall may
cause additional path loss of the order of 1 dB/km.
Path Loss on Non-Line of Sight
Paths
We have spent quite a bit of time
looking at LOS paths, and described the mechanisms which often cause
them to have path loss which differs from the "free space"
assumption. We've seen that the path loss isn't always easy to
predict. When we have a path which is not LOS, it becomes even more
difficult to predict how well signals will propagate over it.
Unfortunately, non-LOS situations are sometimes unavoidable,
particularly in urban areas. The following sections deal with some of
the major factors which must be considered.
Diffraction Losses
In some special cases, such as
diffraction over a single obstacle which can be modeled as a knife
edge, the loss of a non-LOS path can be predicted fairly readily. In
fact, this is the same situation that we saw in Figures 1 and 2, with
the diffraction parameter 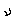 > 0. This parameter, from equation (8), is
> 0. This parameter, from equation (8), is
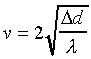
To get  d,
measure the straight-line distance between the endpoints of the link.
Then measure the length of the actual path, which includes the two
endpoints and the tip of the knife edge, and take the difference
between the two. The geometry is shown in Fig. 7(a), the "positive h"
case. A good approximation to the knife-edge diffraction loss in dB
can then be calculated from
d,
measure the straight-line distance between the endpoints of the link.
Then measure the length of the actual path, which includes the two
endpoints and the tip of the knife edge, and take the difference
between the two. The geometry is shown in Fig. 7(a), the "positive h"
case. A good approximation to the knife-edge diffraction loss in dB
can then be calculated from
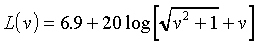 (12)
(12)
Example 3. We want to run a
915 MHz link between two points which are a straight-line distance of
25 km apart. However, 5 km from one end of the link, there is a ridge
which is 100 meters higher than the two endpoints. Assuming that the
ridge can be modeled as a knife edge, and that the paths from the
endpoints to the top of ridge are LOS with adequate Fresnel zone
clearance, what is the expected path loss? From simple geometry, we
find that length of the path over the ridge is 25,001.25 meters, so
that d = 1.25 m. Since 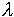 = 0.33 m,
the parameter
= 0.33 m,
the parameter  ,
from (8), is 3.89. Substituting this into (12), we find that the
expected diffraction loss is 24.9 dB. The free space path loss for a
25 km path at 915 MHz is, from equation (6a), 119.6 dB, so the total
predicted path loss for this path is 144.5 dB. This is too lossy a
path for many WLAN devices. For example, suppose we are using WaveLAN
cards with 13 dBi gain antennas, which (disregarding feedline losses)
brings them up to the maximum allowable EIRP of +36 dBm. This will
produce, at the antenna terminals at the other end of the link, a
received power of (36 - 144.5 + 13) = -95.5 dBm. This falls well
short of the -78 dBm requirement of the WaveLAN cards. On the other
hand, a lower-speed system may be quite usable over this path. For
instance, the FreeWave 115 Kbps modems require only about -108 dBm
for reliable operation, which is a comfortable margin below our
predicted signal levels.
,
from (8), is 3.89. Substituting this into (12), we find that the
expected diffraction loss is 24.9 dB. The free space path loss for a
25 km path at 915 MHz is, from equation (6a), 119.6 dB, so the total
predicted path loss for this path is 144.5 dB. This is too lossy a
path for many WLAN devices. For example, suppose we are using WaveLAN
cards with 13 dBi gain antennas, which (disregarding feedline losses)
brings them up to the maximum allowable EIRP of +36 dBm. This will
produce, at the antenna terminals at the other end of the link, a
received power of (36 - 144.5 + 13) = -95.5 dBm. This falls well
short of the -78 dBm requirement of the WaveLAN cards. On the other
hand, a lower-speed system may be quite usable over this path. For
instance, the FreeWave 115 Kbps modems require only about -108 dBm
for reliable operation, which is a comfortable margin below our
predicted signal levels.
To see the effect of operating
frequency on diffraction losses, we can repeat the calculation, this
time using 144 MHz, and find the predicted diffraction loss to be
17.5 dB, or 7.4 dB less than at 915 MHz. At 2.4 GHz, the predicted
loss is 29.0 dB, an increase of 4.1 dB over the 915 MHz case (these
differences are for the diffraction losses only, not the only total
path loss).
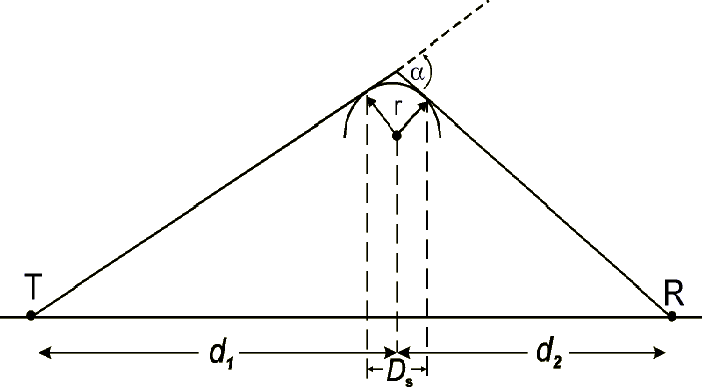
Figure 9 Diffraction
by a Rounded Obstacle
Unfortunately, the paths which
digital experimenters are faced with are seldom this simple. They
will frequently involve diffraction over multiple rooftops or other
obstacles, many of which don't resemble knife edges. The path losses
will generally be substantially greater in these cases than predicted
by the single knife edge model. The paths will also often pass
through objects such as trees and wood-frame buildings which are
semi-transparent at radio frequencies. Many models have been
developed to try and predict path losses in these more complex cases.
The most successful are those which deal with restricted scenarios
rather than trying to cover all of the possibilities. One common
scenario is diffraction over a single obstacle which is too rounded
to be considered a knife edge. There are different ways of treating
this problem; the one described here is from Ref. [3]. The
top of the object is modeled as a cylinder of radius r, as shown in
Fig. 9. To calculate the loss, you need to plot the profile of the
actual object, and then draw straight lines from the link endpoints
such that they just graze the highest part of the object as seen from
their individual perspectives. Then the parameters Ds,
d1, d2 and are estimated, and an estimate of
the radius r can then be calculated from
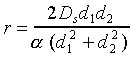 (13)
(13)
Note that the angle is measured in
radians. The procedure then is to calculate the knife edge
diffraction loss for this path as outlined above, and then add to it
an excess loss factor Lex, calculated from
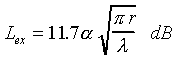 (14)
(14)
There is also a correction factor
for roughness: if the object is, for example, a hill which is
tree-covered rather than smooth at the top, the excess diffraction
loss is said to be about 65% of that predicted in (14). In general,
smoother objects produce greater diffraction losses.
Example 4. We revisit the
scenario in Example 3, but let's suppose that we've now decided that
the ridge blocking our path doesn't cut it as a knife edge (ouch!).
From a plot of the profile, we estimate that Ds = 10
meters. As before, d1 = 20 km, d2 = 5 km and
the height of the ridge is 100 meters. Dusting off our high school
trigonometry, we can work out that 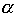 = 1.43, or 0.025 radians. Now, plugging these numbers into (13), we
get r = 188 meters. Then, with
= 1.43, or 0.025 radians. Now, plugging these numbers into (13), we
get r = 188 meters. Then, with 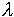 = 0.33 m, we can calculate the excess loss from (14):
= 0.33 m, we can calculate the excess loss from (14):
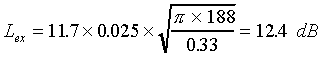
So, summed with the knife edge
loss calculated previously, we have an estimated total diffraction
loss of 37.3 dB (assuming the ridge is "smooth" rather than "rough").
This is a lot, but you can easily imagine scenarios where the losses
are much greater: just look at the direct dependence on the angle in
(14) and picture from Fig. 9 what happens when the obstacle is closer
to one of the link endpoints. Amateurs doing weak signal work are
accustomed to dealing with large path losses in non-LOS propagation,
but such losses are usually intolerable in high-speed digital
links.
Attenuation from Trees and
Forests
Trees can be a significant source
of path loss, and there are a number of variables involved, such as
the specific type of tree, whether it is wet or dry, and in the case
of deciduous trees, whether the leaves are present or not. Isolated
trees are not usually a major problem, but a dense forest is another
story. The attenuation depends on the distance the signal must
penetrate through the forest, and it increases with frequency.
According to a CCIR report [10], the attenuation is of the
order of 0.05 dB/m at 200 MHz, 0.1 dB/m at 500 MHz, 0.2 dB/m at 1
GHz, 0.3 dB/m at 2 GHz and 0.4 dB/m at 3 GHz. At lower frequencies,
the attenuation is somewhat lower for horizontal polarization than
for vertical, but the difference disappears above about 1 GHz. This
adds up to a lot of excess path loss if your signal must
penetrate several hundred meters of forest! Fortunately, there is
also significant propagation by diffraction over the treetops,
especially if you can get your antennas up near treetop level or keep
them a good distance from the edge of the forest, so all is not lost
if you live near a forest.
General Non-LOS Propagation
Models
There are many more general models
and empirical techniques for predicting non-LOS path losses, but the
details are beyond the scope of this paper. Most of them are aimed at
prediction of the paths between elevated base stations and mobile or
portable stations near ground level, and they typically have
restrictions on the frequency range and distances for which they are
valid; thus they may be of limited usefulness in the planning of
amateur high-speed digital links. Nevertheless, they are well worth
studying to gain further insight into the nature of non-LOS
propagation. The details are available in many texts - Ref.
[3] has a particularly good treatment. One crude, but useful,
approximation will be mentioned here: the loss on many non-LOS paths
in urban areas can be modeled quite well by a fourth-power distance
law. In other words, we substitute d4 for d2 in
equation (5). In equation (6), we can substitute 40log(d) for the
20log(d) term, which would correspond to the assumption of square-law
distance loss for distances up to 1 km (or 1 mile, for the non-metric
version of the equation), and fourth-law loss thereafter. This is
probably an overly optimistic assumption for heavily built-up areas,
but is at least a useful starting point.
The propagation losses on non-LOS
paths can be discouragingly high, particularly in urban areas.
Antenna height becomes a critical factor, and getting your antennas
up above rooftop heights will often spell the difference between
success and failure. Due to the great variability of propagation in
cluttered urban environments, accurate path loss predictions can be
difficult. If a preliminary analysis of the path indicates that you
are at least in the ballpark (say within 10 or 15 dB) of having a
usable link, then it will generally be worthwhile to give it a try
and hope to be pleasantly surprised (but be prepared to be
disappointed!).
Software Tools for
Propagation Prediction
Although there is no substitute
for experience and acquiring a "feel" for radio propagation, computer
programs can make the job of predicting radio link performance a lot
easier. They are particularly handy for exploring "what if" scenarios
with different paths, antenna heights, etc. Unfortunately, they also
tend to cost money! If you're lucky, you may have access to one of
the sophisticated prediction programs which includes the most complex
propagation models, terrain databases, etc. If not, you can still
find some free software utilities that will make it easier to do some
of the calculations discussed above, such as knife edge diffraction
losses. One very useful freeware program which was developed
specifically for short-range VHF/UHF applications is RFProp,
by Colin Seymour, G4NNA. Check Colin's Web
page at
http://www.users.dircon.co.uk/~netking/freesw.htm for more
information and downloading instructions. This is a Windows (3.1, 95
or NT) program which can calculate path loss in free space and simple
diffraction scenarios. In addition to calculating knife edge
diffraction loss, it provides some correction factors for estimating
the loss caused by more rounded objects, such as hills. It also
allows changing the distance loss exponent from square-law to
fourth-law (or anything else, for that matter) to simulate long paths
with ground reflections or obstructed urban paths. There is also some
provision for estimating the loss caused when the signals must
penetrate buildings. The program has a graphical user interface in
which the major path parameters can be entered and the result (in
terms of receiver SNR margin) seen immediately. There is also a
tabular output which lists the detailed results along with all of the
assumed parameters.
Special Considerations
for Digital Systems
We have previously looked at the
effect of multipath on path loss. When reflections occur from objects
which are very close to the direct path, then paths have very similar
lengths and nearly the same time delay. Depending on the relative
phase shifts of the paths, the signals traversing them at a given
frequency can add constructively to provide a gain with respect to a
single path, or destructively to provide a loss. On longer paths in
particular, the effect is usually a loss. Since the path lengths are
nearly equal, the loss occurs over a wide frequency range, producing
a "flat" fade.
In many cases, however,
reflections from objects well away from the direct path can give rise
to significant multipath. The most common reflectors are buildings
and other manmade structures, but many natural features can also be
good reflectors. In such cases, the propagation delays of the paths
from one end of the link to the other can differ considerably. The
extent of this time spreading of the signal is commonly measured by a
parameter known as the delay spread of the path. One
consequence of having a larger delay spread is that the reinforcement
and cancellation effects will now vary more rapidly with frequency.
For example, suppose we have two paths with equal attenuation and
which differ in length by 300 meters, corresponding to a delay
difference of 1 µsec. In the frequency domain, this link will
have deep nulls at intervals of 1 MHz, with maxima in between. With a
narrowband system, you may be lucky and be operating at a frequency
near a maximum, or you may be unlucky and be near a null, in which
case you lose most of your signal (techniques such as space diversity
reception may help, though). The path loss in this case is highly
frequency-dependent. On the other hand, a wideband signal which is,
say, several MHz wide, would be subject to only partial cancellation
or selective fading. Depending on the nature of the signal and
how information is encoded into it, it may be quite tolerant of
having part of its energy notched out by the multipath channel.
Tolerance of multipath-induced signal cancellation is one of the
major benefits of spread spectrum (SS) transmission techniques.
Longer multipath delay spreads
have another consequence where digital signals are concerned,
however: overlap of received data symbols with adjacent symbols,
known as intersymbol interference or ISI. Suppose we try to
transmit a 1 Mbps data stream over the two-path multipath channel
mentioned above. Assuming a modulation scheme with 1 sec symbol
length is used, then the signals arriving over the two paths will be
offset by exactly one symbol period. Each received symbol arriving
over the shorter path will be overlaid by a copy of the previous
symbol from the longer path, making it impossible to decode with
standard demodulation techniques. This problem can be solved by using
an adaptive equalizer in the receiver, but this level of
sophistication is not commonly found in amateur or WLAN modems (but
it will certainly become more common as speeds continue to increase).
Another way to attack this problem is to increase the symbol length
while maintaining a high bit rate by using a multicarrier modulation
scheme such as OFDM (Orthogonal Frequency Division Multiplex), but
again, such techniques are seldom found in the wireless modem
equipment available to hobbyists. For unequalized multipath channels,
the delay spread must be much less than the symbol length, or the
link performance will suffer greatly. The effect of multipath-induced
ISI is to establish an irreducible error rate - beyond a
certain point, increasing transmitter power will cause no improvement
in BER, since the BER vs Eb/N0 curve has gone
flat. A common rule of thumb prescribes that the multipath delay
spread should be no more than about 10% of the symbol length. This
will generally keep the irreducible error rate down to the order of
10-3 or less. Thus, in our two-path example above, a
system running at 100K symbols/s or less may work satisfactorily. The
actual raw BER requirements for a particular system will of course
depend on the error-control coding technique used.
Although it is commonly believed
that SS modulation schemes solve the multipath ISI problem, this is
not really the case. As stated above, SS can convert a flat-faded
channel into one which has selective fading, which is a good thing.
In the case of Frequency Hopping (FHSS), it means that signal
cancellation due to multipath will occur only a fraction of the time
(i.e., only on some of the channels we hop to), and we can recover
the data by means of Forward Error Correction (or by error detection
and retransmission). In the case of Direct Sequence (DSSS), only a
fraction of the transmitted spectrum is notched out by the multipath
cancellation. This causes some degradation of the BER, but again
error control coding can be used to compensate for this. In both
cases, SS modulation has given us a form of frequency diversity. For
DSSS, the large continuous spread bandwidth allows us to resolve many
of the multipath components (those separated by delays of
approximately the reciprocal of the spread bandwidth, or more). These
appear as separate peaks in the DSSS receiver correlator output. A
diversity receiver using the RAKE principle can take advantage of
some of the multipath signal power by combining it constructively
before making the bit decisions. More commonly, however, only the
largest correlation peak is used, and all of the other multipath
energy represents wideband interference. Regardless of whether a
diversity receiver structure is used, however, ISI (and hence BER
degradation) will still occur when the multipath delay
spread approaches the same order of magnitude as the information
symbol length. An excellent discussion of these concepts can be found
in chapter 9 of Ref. [11].
As an illustration, consider again
the WaveLAN product, which is a DSSS system using DQPSK modulation, a
spread bandwidth of 11 MHz, and a symbol length of 1 µsec. Tests
of WaveLAN using a channel simulator [12] have shown that its
performance degrades when the delay spread exceeds 84 nsec (0.084
µsec), which is only about 10% of the symbol length.
Delay spreads of several
microseconds are not uncommon, especially in urban areas. Mountainous
areas can produce much longer delay spreads, sometimes tens of
microseconds. This spells big trouble for doing high-speed data
transmission in these areas. The best way to mitigate multipath in
these situations is to use highly directional antennas, preferably at
both ends of the link. The higher the data rate, the more critical it
becomes to use high-gain antennas. This is one advantage to going
higher in frequency. The delay spread for a given link will usually
not exhibit much frequency dependence - for example, there will be
similar amounts of multipath whether you operate at 450 MHz or 2.4
GHz, if you use the same antenna gain and type. However, you
can get more directivity at the higher frequencies, which often will
result in significantly reduced multipath delay spread and hence
lower BER. It may seem strange that high-speed WLAN products are
often supplied with omnidirectional antennas which do nothing to
combat multipath, but this is because the antennas are intended for
indoor use. The attenuation provided by the building structure will
usually cause a drastic reduction in the amplitude of reflections
from outside the building, as well as from distant areas inside the
building. Delay spreads therefore tend to be much smaller inside
buildings - typically of the order of 0.1 µsec or less. However,
as WLAN products with data rates of 10 Mbps and beyond are now
appearing, even delay spreads of this magnitude are problematic and
must be dealt with by such measures as equalizers, high-level
modulation schemes and sectorized antennas.
Conclusions
Radio propagation is a vast topic,
and we've only scratched the surface here. We haven't considered, for
example, the interesting area of data transmission involving mobile
stations - maybe next year! Hopefully, this paper has provided some
insight into the problems and solutions associated with setting up
digital links in the VHF to microwave spectrum. To sum up, here are a
few guidelines and principles:
- Always strive for LOS
conditions. Even with LOS, you must pay attention to details
regarding variability of refractivity, Fresnel zone clearance and
avoiding reflections from the ground and other surfaces. Non-LOS
paths will often lead to disappointment unless they are very
short, especially with the high-speed unlicenced WLAN devices.
Their low ERP limits and high receive signal power requirements
(due to large noise bandwidths, high noise figures and sometimes,
significant modem implementation losses) leave little margin for
higher-than-LOS path losses. Hams are not encumbered by the low
ERP limits, but it can be very expensive to overcome excessive
path losses with higher transmitter powers.
- Use as much antenna gain as is
practical. It is always worthwhile to try both polarizations, but
horizontal polarization will often be superior to vertical. It
will generally provide less multipath in urban areas, and may
provide lower path loss in some non-LOS situations (e.g.,
attenuation from trees at VHF and lower UHF). Also, interfering
signals from pagers and the like tend to be vertically polarized,
so using the opposite polarization can often provide some
protection from them.
- There are advantages to going
higher in frequency, into the microwave bands, due to the higher
antenna gains which can be achieved. The tighter focusing of
energy which can be achieved may result in lower overall path loss
on LOS paths (providing that you can keep the feedline losses
under control), and less multipath. Higher frequencies also have
smaller Fresnel zones, and thus require less clearance over
obstacles to avoid diffraction losses. And, of course, the higher
bands have more bandwidth available for high-speed data, and less
probability of interference. However, the advantage may be lost in
non-LOS situations, since diffraction losses, and attenuation from
natural objects such as trees, increase with
frequency.
Radio propagation is seldom 100%
predictable, and one should never hesitate to experiment. It's very
useful, though, to be equipped with enough knowledge to know what
techniques to try, and when there is little probability of success.
This paper was intended to help fill some gaps in that knowledge.
Good luck with your radio links!
Acknowledgements
The author gratefully acknowledges the work of his daughter
Kelly
(http://hydra.carleton.ca/~klm) in producing the figures for this
paper. WaveLAN is a registered trademark of Lucent Technologies,
Inc.
References
[1] ARRL UHF/Microwave Experimenter's Manual
(American Radio Relay League, 1990).
[2] Hall, M.P.M., Barclay, L.W. and Hewitt, M.T. (Eds.),
Propagation of Radiowaves (Institution of Electrical
Engineers, 1996).
[3] Parsons, J.D., The Mobile Radio Propagation Channel
(Wiley & Sons, 1992).
[4] Doble, J., Introduction to Radio Propagation for
Fixed and Mobile Communications (Artech House, 1996).
[5] Bertoni, H.L., Honcharenko, W., Maciel, L.R. and Xia,
H.H., "UHF Propagation Prediction for Wireless Personal
Communications", Proceedings of the IEEE, Vol. 82, No. 9,
September 1994, pp. 1333-1359.
[6] Andersen, J.B., Rappaport, T.S. and Yoshida, S.,
"Propagation Measurements and Models for Wireless Communications
Channels", IEEE Communications Magazine, January 1995, pp.
42-49.
[7] Freeman, R.L., Radio System Design for
Telecommunications (Wiley & Sons, 1987).
[8] Lee, W.C.Y., Mobile Communications Design
Fundamentals, Second Edition (Wiley & Sons, 1993).
[9] CCIR (now ITU-R) Report 567-4, "Propagation data and
prediction methods for the terrestrial land mobile service using the
frequency range 30 MHz to 3 GHz" (International Telecommunication
Union, Geneva, 1990).
[10] CCIR Report 1145, "Propagation over irregular terrain
with and without vegetation" (International Telecommunication Union,
Geneva, 1990).
[11] Pahlavan, K., and Levesque, A.H., Wireless
Information Networks (Wiley & Sons, 1995).
[12] Hollemans, W., and Verschoor, A., "Performance Study
of WaveLAN and Altair Radio-LANs", Proceedings of the 5th IEEE
Symposium on Personal, Indoor and Mobile Radio Communications,
September 1994.
Appendix
|
Cable Type
|
144 MHz
|
220 MHz
|
450 MHz
|
915 MHz
|
1.2 GHz
|
2.4 GHz
|
5.8 GHz
|
|
RG-58
|
6.2
(20.3)
|
7.4
(24.3)
|
10.6
(34.8)
|
16.5
(54.1)
|
21.1
(69.2)
|
32.2
(105.6)
|
51.6
(169.2)
|
|
RG-8X
|
4.7
(15.4)
|
6.0
(19.7)
|
8.6
(28.2)
|
12.8
(42.0)
|
15.9
(52.8)
|
23.1
(75.8)
|
40.9
(134.2)
|
|
LMR-240
|
3.0
(9.8)
|
3.7
(12.1)
|
5.3
(17.4)
|
7.6
(24.9)
|
9.2
(30.2)
|
12.9
(42.3)
|
20.4
(66.9)
|
|
RG-213/214
|
2.8
(9.2)
|
3.5
(11.5)
|
5.2
(17.1)
|
8.0
(26.2)
|
10.1
(33.1)
|
15.2
(49.9)
|
28.6
(93.8)
|
|
9913
|
1.6
(5.2)
|
1.9
(6.2)
|
2.8
(9.2)
|
4.2
(13.8)
|
5.2
(17.1)
|
7.7
(25.3)
|
13.8
(45.3)
|
|
LMR-400
|
1.5
(4.9)
|
1.8
(5.9)
|
2.7
(8.9)
|
3.9
(12.8)
|
4.8
(15.7)
|
6.8
(22.3)
|
10.8
(35.4)
|
|
3/8" LDF
|
1.3
(4.3)
|
1.6
(5.2)
|
2.3
(7.5)
|
3.4
(11.2)
|
4.2
(13.8)
|
5.9
(19.4)
|
8.1
(26.6)
|
|
LMR-600
|
0.96
(3.1)
|
1.2
(3.9)
|
1.7
(5.6)
|
2.5
(8.2)
|
3.1
(10.2)
|
4.4
(14.4)
|
7.3
(23.9)
|
|
1/2" LDF
|
0.85
(2.8)
|
1.1
(3.6)
|
1.5
(4.9)
|
2.2
(7.2)
|
2.7
(8.9)
|
3.9
(12.8)
|
6.6
(21.6)
|
|
7/8" LDF
|
0.46
(1.5)
|
0.56
(2.1)
|
0.83
(2.7)
|
1.2
(3.9)
|
1.5
(4.9)
|
2.3
(7.5)
|
3.8
(12.5)
|
|
1 1/4" LDF
|
0.34
(1.1)
|
0.42
(1.4)
|
0.62
(2.0)
|
0.91
(3.0)
|
1.1
(3.6)
|
1.7
(5.6)
|
2.8
(9.2)
|
|
1 5/8" LDF
|
0.28
(0.92)
|
0.35
(1.1)
|
0.52
(1.7)
|
0.77
(2.5)
|
0.96
(3.1)
|
1.4
(4.6)
|
2.5
(8.2)
|
Table 1 - Attenuation of Various Transmission Lines in
Amateur and ISM Bands in dB/ 100 ft (dB/ 100 m)
Notes
Attenuation data based on figures from the "Communications
Coax Selection Guide" from Times Microwave Systems
(http://www.timesmicrowave.com/products/commercial/selectguide/atten/)
and other sources.
The LMR series is manufactured by Times
Microwave. 9913 is manufactured by Belden Corp. RG-series cables are
manufactured by Belden and many others. The LDF
series are foam dielectric, solid corrugated outer conductor cables,
best known by the brand name HELIAX (®Andrew
Corp.).
 Back
to the School Home Page
Back
to the School Home Page
updated 20 February
2001, © 2001 ICTP-ARPL, HTML by cfonda
![]()

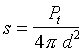 (1)
(1)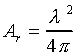 (3)
(3)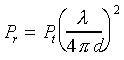 (4)
(4)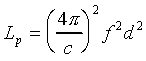 (5)
(5)





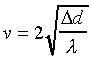 (8)
(8)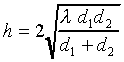 (9)
(9)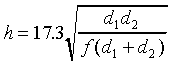 (10a)
(10a)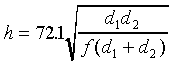 (10b)
(10b)

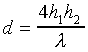 (11)
(11)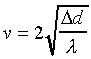

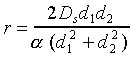 (13)
(13)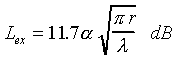 (14)
(14)